Embark on a statistical adventure with AP Stats Chapter 2, where we delve into the art of exploring and understanding data through graphical representations and numerical summaries. From histograms to scatterplots, from mean to standard deviation, this chapter empowers us to uncover hidden patterns and make informed decisions based on data.
Get ready to unravel the secrets of data analysis, as we navigate the intricacies of probability distributions and discover the power of statistical inference. Join us on this captivating journey through the realm of statistics!
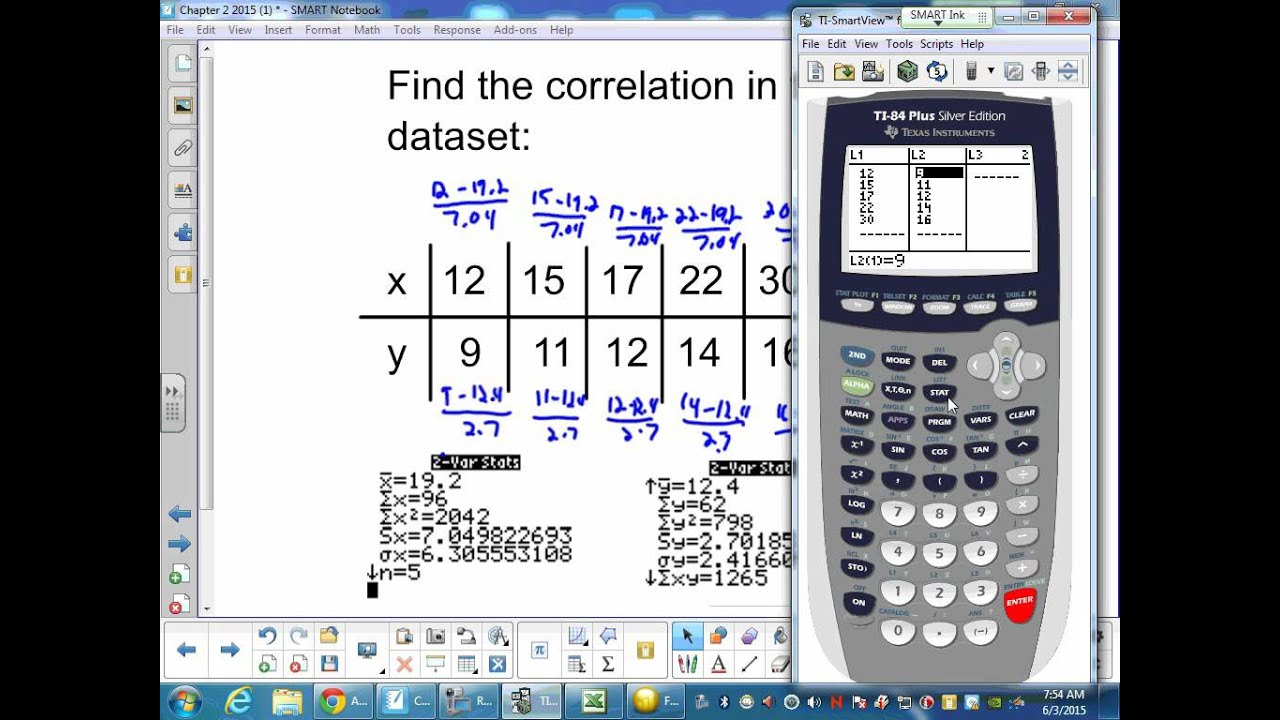
Exploratory Data Analysis

Exploratory Data Analysis (EDA) is a crucial step in data analysis that helps us understand the characteristics of our data, identify patterns, and uncover hidden insights. It involves using various techniques to visualize and summarize data, enabling us to make informed decisions and draw meaningful conclusions.
AP Stats Chapter 2 provides an in-depth look at probability distributions, but for a change of pace, check out drug eating genius mage chapter 1 for a magical adventure. Once you’ve explored the realm of fantasy, return to AP Stats Chapter 2 to master the fundamentals of statistical distributions.
EDA plays a vital role in AP Statistics Chapter 2, as it provides a foundation for understanding the concepts of probability and statistical inference. By exploring our data, we can gain insights into its distribution, variability, and relationships between variables.
Graphical Techniques
- Stem-and-Leaf Plots: Stem-and-leaf plots are a graphical representation of data that shows the distribution of values. They provide a quick and easy way to identify patterns, outliers, and the overall shape of the data.
- Histograms: Histograms are bar graphs that show the frequency of data values occurring within specified intervals. They help us visualize the distribution of data and identify any potential outliers.
- Box Plots: Box plots are graphical representations that show the median, quartiles, and range of data. They are useful for comparing multiple data sets and identifying outliers.
- Scatterplots: Scatterplots are graphs that show the relationship between two variables. They can reveal linear or nonlinear trends, as well as identify outliers and potential correlations.
Numerical Techniques
- Measures of Central Tendency: Measures of central tendency, such as mean, median, and mode, provide a single value that represents the “center” of the data. They help us understand the typical value of the data.
- Measures of Variability: Measures of variability, such as range, variance, and standard deviation, provide information about how spread out the data is. They help us understand the consistency of the data.
- Quartiles and Percentiles: Quartiles and percentiles divide data into equal parts. They help us identify the median and other important values within the data set.
Graphical Representations of Data

Graphical representations are powerful tools for summarizing and visualizing data. They allow us to see patterns, trends, and relationships that might not be apparent from the raw data alone. In AP Statistics Chapter 2, we will explore three common types of graphical representations: histograms, box plots, and scatterplots.
Histograms
A histogram is a graphical representation of the distribution of a quantitative variable. It is constructed by dividing the range of the data into a number of equal-width intervals and then counting the number of data points that fall into each interval. The resulting bars are then plotted, with the height of each bar representing the frequency of the corresponding interval.
Histograms can be used to see the shape of a distribution, identify outliers, and compare the distributions of two or more groups. To create a histogram using HTML table tags, you can use the following code:
“`html
| Interval | Frequency |
|---|---|
| [interval 1] | [frequency 1] |
| [interval 2] | [frequency 2] |
“`
Box Plots
A box plot is a graphical representation of the distribution of a quantitative variable. It is constructed by finding the minimum, maximum, median, and quartiles of the data. The box plot is then drawn with a line representing the median, a box representing the interquartile range (IQR), and whiskers extending to the minimum and maximum values.
Box plots can be used to see the shape of a distribution, identify outliers, and compare the distributions of two or more groups. To create a box plot using HTML table tags, you can use the following code:
“`html
| Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|
| [minimum] | [Q1] | [median] | [Q3] | [maximum] |
“`
Scatterplots
A scatterplot is a graphical representation of the relationship between two quantitative variables. It is constructed by plotting the data points on a coordinate plane, with the x-axis representing one variable and the y-axis representing the other variable. The resulting plot can be used to see the direction and strength of the relationship between the two variables.
Scatterplots can be used to identify trends, correlations, and outliers. To create a scatterplot using HTML table tags, you can use the following code:
“`html
| Variable 1 | Variable 2 |
|---|---|
| [value 1, variable 1] | [value 1, variable 2] |
| [value 2, variable 1] | [value 2, variable 2] |
“`
By using these graphical representations, we can gain a deeper understanding of the data we are working with. They can help us to identify patterns, trends, and relationships that might not be apparent from the raw data alone.
Ap Stats Chapter 2, as you know, is a bit tricky. It’s easy to get lost in the formulas and calculations, but it’s important to remember the big picture. Just like in kanojo mo kanojo chapter 142 , where the characters are trying to find their way through a complicated situation, in Ap Stats Chapter 2, we’re trying to find our way through a complicated subject.
But don’t worry, with a little bit of effort, we can both make it through.
Numerical Summaries of Data: Ap Stats Chapter 2

Numerical summaries provide concise descriptions of the central tendencies and spread of data. They help us understand the overall pattern and variability within a dataset.
In the midst of delving into the intricacies of AP Stats Chapter 2, one might find respite in exploring the captivating rhythm of war chapter summaries . The epic fantasy unfolds in intricate detail, providing a welcome distraction from the statistical analysis and probability calculations that await in AP Stats Chapter 2.
Measures of Central Tendency
Measures of central tendency indicate the “typical” value in a dataset. They include:
- Mean: The average value, calculated by summing all values and dividing by the number of values.
Mean = (Σx) / n
- Median: The middle value when the data is arranged in ascending order. If there are two middle values, the median is their average.
- Mode: The value that occurs most frequently in a dataset.
Measures of Spread, Ap stats chapter 2
Measures of spread describe how the data is distributed around the central tendency. They include:
- Range: The difference between the maximum and minimum values.
- Variance: The average squared difference between each value and the mean.
Variance = (Σ(x – μ)^2) / (n-1)
- Standard Deviation: The square root of the variance, which measures the typical distance of values from the mean.
Interpretation and Application
Numerical summaries help us:
- Compare different datasets.
- Identify outliers or unusual values.
- Make inferences about the population from which the data was sampled.
- Create statistical models and perform hypothesis testing.
Probability Distributions
Probability distributions are mathematical functions that describe the probability of different outcomes in a random experiment. They play a crucial role in AP Statistics Chapter 2, as they allow us to predict the likelihood of certain events occurring.
Different types of probability distributions exist, each with its own characteristics. Two commonly encountered distributions are the binomial distribution and the normal distribution. The binomial distribution models the number of successes in a sequence of independent experiments, while the normal distribution models continuous data that is often bell-shaped.
Using probability distributions, we can calculate the probability of specific outcomes or events. This information is essential for making informed decisions and drawing meaningful conclusions from data.
Closing Summary

As we conclude our exploration of AP Stats Chapter 2, we emerge with a newfound appreciation for the power of data analysis. Graphical representations and numerical summaries have become our tools to illuminate patterns, draw meaningful conclusions, and make predictions. Embracing the principles of this chapter, we are now equipped to navigate the complexities of data-driven decision-making, unlocking a world of possibilities.